Arrays - Concept And Techniques
A comprehensive guide on various array operations and techniques used in algorithm design, particularly for solving problems efficiently
Main Concepts:
Array: A collection of elements (values or variables), each identified by an array index or key. The elements are stored in contiguous memory locations.
Understanding Row-Major Order
Concept: In a 2D array, for instance, the entire first row is stored in contiguous memory locations, followed by the entire second row, and so on.
Memory Layout:
Consider a 2D array
arr[3][2](3 rows and 2 columns).The memory layout will be:
arr[0][0], arr[0][1], arr[1][0], arr[1][1], arr[2][0], arr[2][1].
Access Pattern:
Access is row-wise.
When you traverse the array, you complete one row before moving to the next.
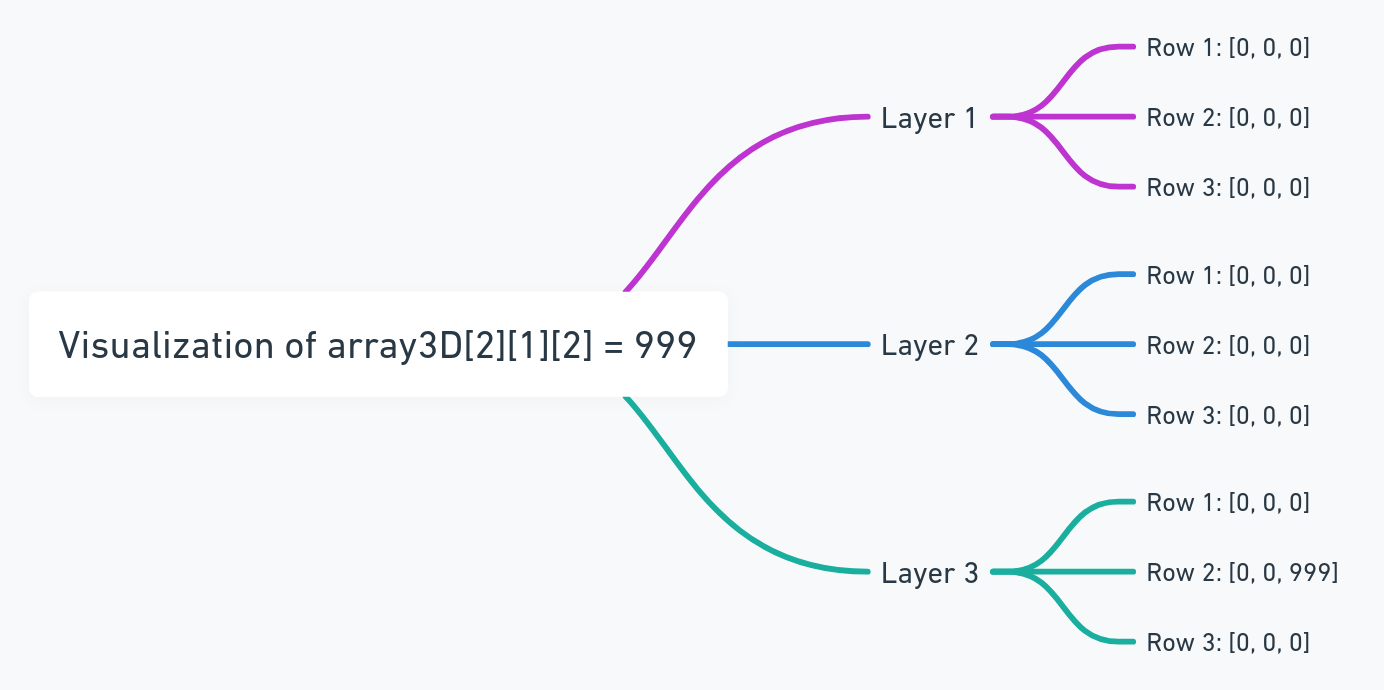
In a 3D array, you can think of the structure as having layers, rows, and columns:
Layers: These are like different 2D arrays stacked on top of each other. Each layer can be thought of as a separate page or level.
Rows: Within each layer, you have rows. These are similar to rows in a 2D array or a spreadsheet, extending horizontally.
Columns: Within each row, you have columns. These extend vertically within a layer.
So, when you access an element in a 3D array, you specify its position in terms of the layer it's in, the row within that layer, and the column within that row.
For example, In this visualization, the element at the 3rd layer, 2nd row, and 3rd column is set to 999, while the other elements are assumed to be initialized to 0 for simplicity.
Array Operations :
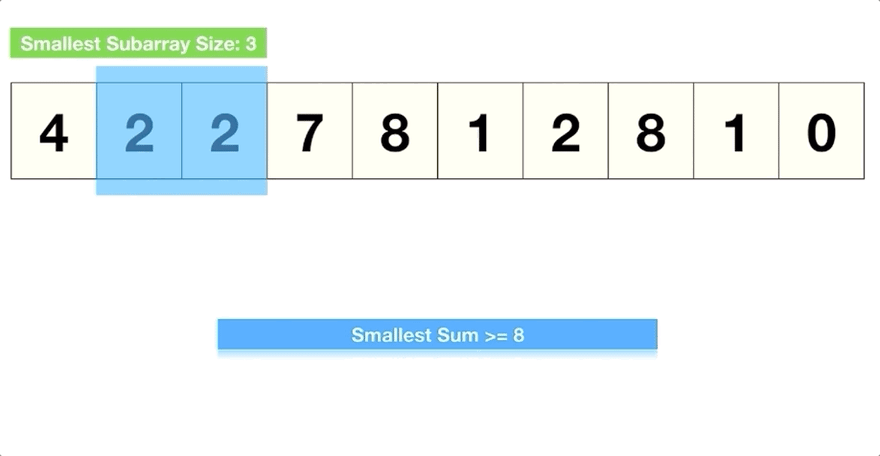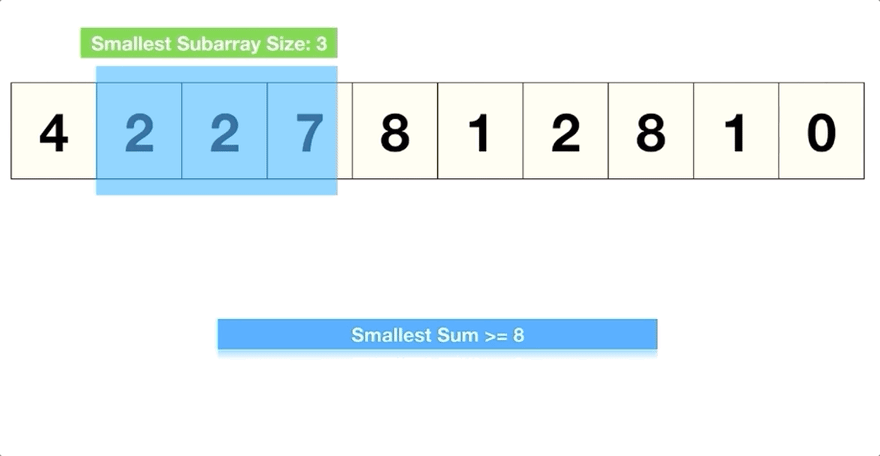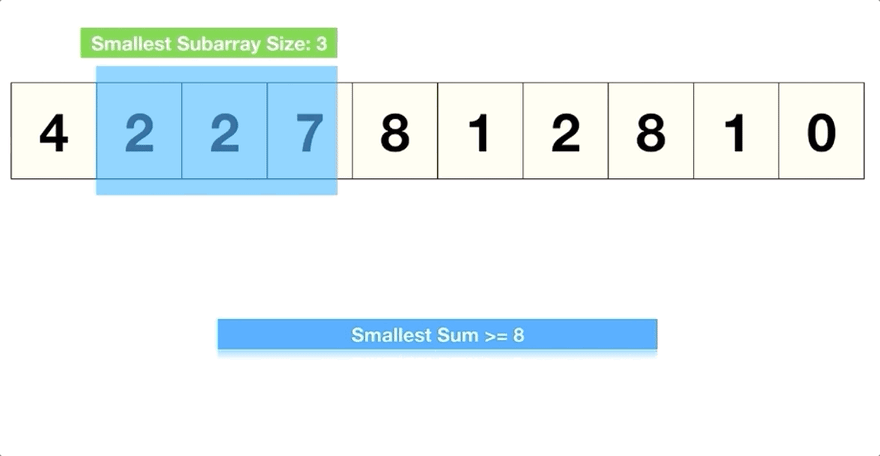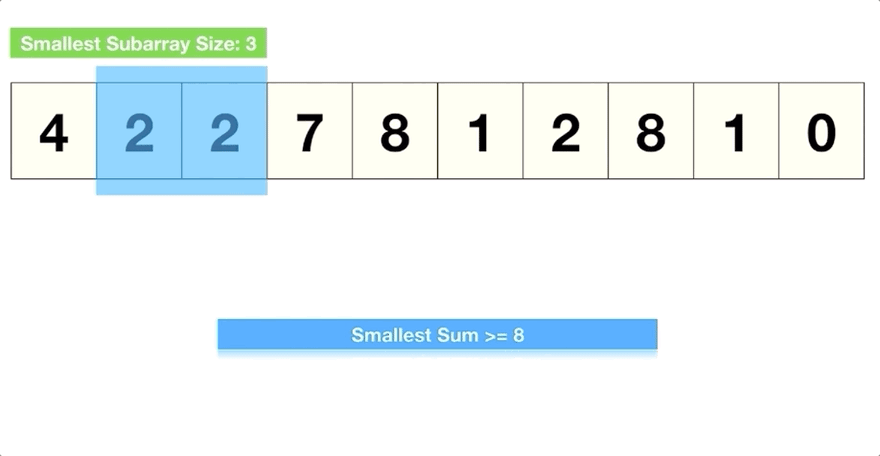
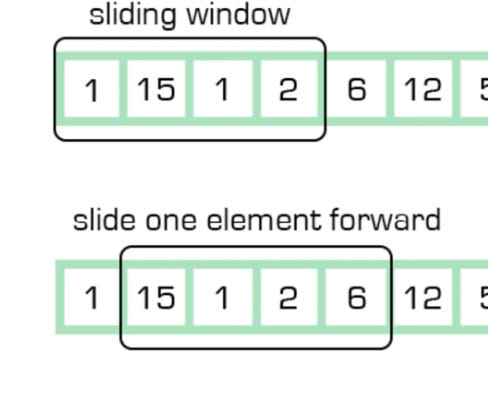
Sliding window
The sliding window technique is a method often used in algorithm design, especially for solving problems that involve arrays or lists. This technique can be particularly effective for problems that ask for things like the longest or shortest subarray that meets certain criteria, or for problems that involve contiguous sequences of elements.
Concept:
Imagine a window that slides over your data (like an array). This window can expand or contract depending on the problem requirements. The "window" is a subarray or a subset of your data.
Key Characteristics:
1. **Variable or Fixed Size**: The window might have a fixed size, which stays constant as it slides, or a variable size, which can expand or contract during the execution of the algorithm.
2. **Efficiency**: The sliding window technique can help reduce the time complexity from O(n²) to O(n) for certain problems, making it a powerful tool for optimizing solutions.
3. **Two Pointers**: Often implemented using two pointers (or indices) that represent the start and end of the window.
Common Use Cases:
1. **Maximum/Minimum Sum of Subarray**: Find the maximum or minimum sum of all subarrays of a fixed size.
2. **Longest/Shortest Substring with K Distinct Characters**: Find the longest or shortest substring that contains exactly K distinct characters.
3. **Subarray with Given Sum**: Find a contiguous subarray that sums up to a given value.
Example:
Consider an array and a problem where you need to find the maximum sum of any contiguous subarray of size `k`.
- You start with a window covering the first `k` elements and calculate their sum.
- Then, slide the window one element to the right, subtract the element that is no longer in the window, and add the new element that is now included in the window.
- Continue this process throughout the array, keeping track of the maximum sum you encounter.
This approach is much more efficient than calculating the sum of every possible subarray of size `k`, which would be a more brute-force approach.
Let's consider a simple example to demonstrate the sliding window technique in JavaScript
function maxSumSubarray(arr, k) {
let maxSum = 0;
let windowSum = 0;
// Calculate the sum of the first window
for (let i = 0; i < k; i++) {
windowSum += arr[i];
}
maxSum = windowSum;
// Slide the window; subtract the element going out and add the element coming in
for (let i = k; i < arr.length; i++) {
windowSum += arr[i] - arr[i - k];
maxSum = Math.max(maxSum, windowSum);
}
return maxSum;
}
// Example usage
const arr = [1, 2, 3, 4, 5, 6, 7];
const k = 3;
console.log(maxSumSubarray(arr, k)); // Output will be the maximum sum of any subarray of size 3
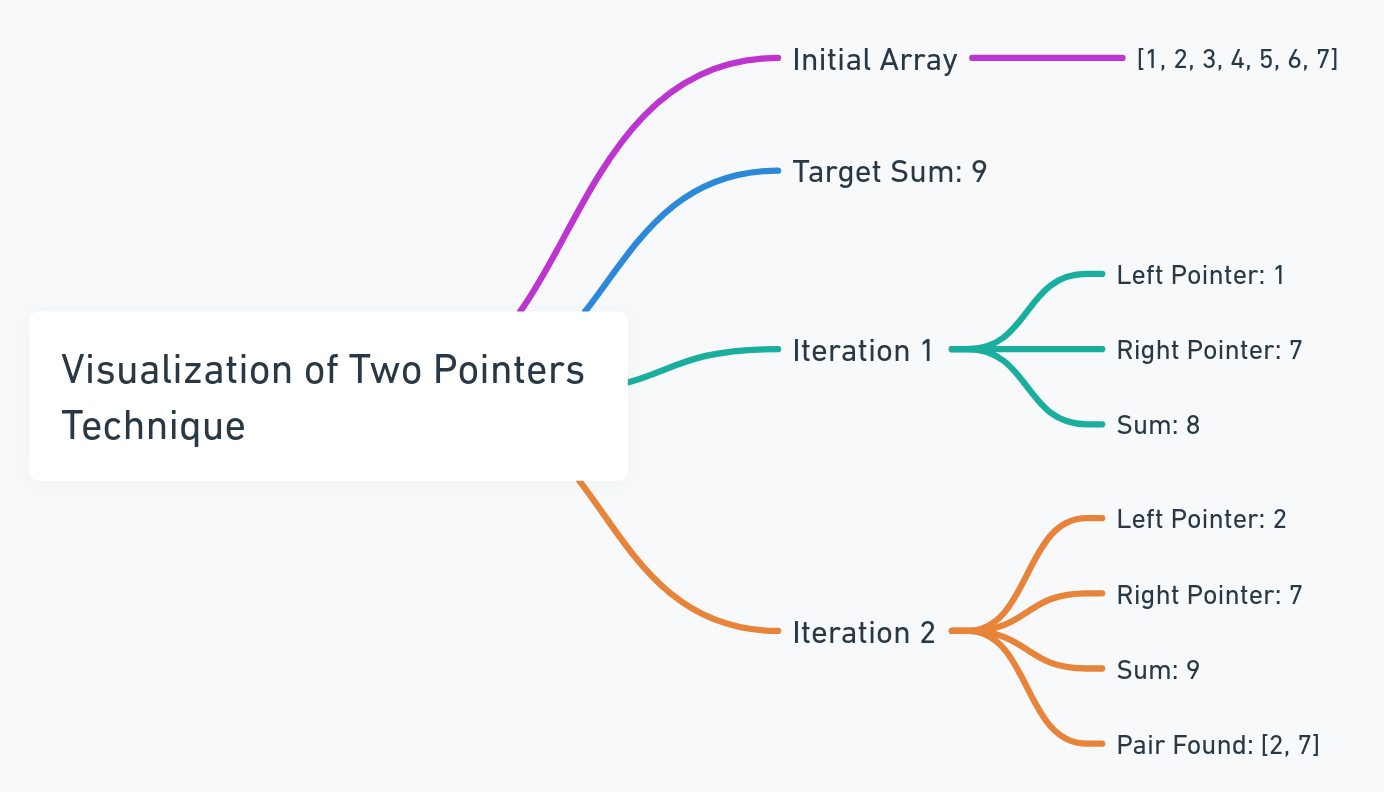
Two pointers
The two pointers technique is a common method used in algorithms to solve problems efficiently by using two pointers (or indices) to traverse an array (or two arrays). This technique can simplify the logic and reduce the time complexity of certain problems.
Efficiency: This method can often reduce the time complexity from O(n²) to O(n) for certain problems.
Basic Concept:
Two Pointers in a Single Array: Often used in problems involving a sorted array where you need to find a pair of elements that meet certain criteria. The pointers typically start at opposite ends of the array and move towards each other.
Two Pointers in Two Arrays: Used when you have two arrays and need to compare or merge them. Each array has its own pointer, and you move these pointers independently based on your algorithm's logic.
Let's write a simple JavaScript function to demonstrate the two pointers technique for finding a pair of numbers in a sorted array that add up to a specific target. Here's an example:
Example:
function findPairWithSum(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left < right) {
const sum = arr[left] + arr[right];
if (sum === target) {
return [arr[left], arr[right]];
} else if (sum < target) {
left++; // Move the left pointer forward
} else {
right--; // Move the right pointer backward
}
}
return null; // Return null if no pair is found
}
// Example usage
const sortedArray = [1, 2, 3, 4, 5, 6, 7];
const targetSum = 9;
console.log(findPairWithSum(sortedArray, targetSum)); // Output will be a pair like [2, 7] or null if no pair is found
while both Two Pointers and Sliding Window involve traversing through a sequence, Two Pointers typically involve individual pointers moving and making decisions based on elements at their specific locations, while Sliding Window involves managing a subset of the sequence as a single entity and maintaining information about that subset as it changes.
Traversing from the right
in some scenarios, it's more efficient or logical to start at the end of the array and move towards the beginning.
The technique of "Traversing from the Right" in an array is a straightforward concept. Typically, when we process arrays, we start at the beginning (the left side) and move towards the end (the right side).
Key Points:
1. **Start at the End**: You initialize your pointer or index at the last element of the array (the rightmost element).
2. **Move Backwards**: Instead of incrementing the index (as you would in a left-to-right traversal), you decrement it, moving from right to left through the array.
3. **Use Cases**: This approach is often used in problems where the solution depends on elements that come later in the array. For example:
- **Daily Temperatures Problem**: You might want to find out how many days you have to wait for a warmer temperature. Starting from the right makes it easier to keep track of the temperatures you've already seen and calculate the waiting days.
- **Number of Visible People in a Queue**: If you're trying to determine how many people can be seen in a queue from the back, starting from the right allows you to process each person and compare them with those already seen.
Advantages:
- **Efficiency**: In some problems, starting from the end of the array can lead to more efficient solutions, avoiding the need for additional data structures or nested loops.
- **Simplicity**: For certain problems, this approach can simplify the logic and make the solution more intuitive.
Example:
Here's a simple example in pseudocode to illustrate the concept:
```pseudocode
array = [A, B, C, D, E]
index = length of array - 1 // Start from the rightmost element
while index >= 0:
process(array[index])
index = index - 1 // Move to the left
```
In this example, you start processing the array from element 'E' and move leftwards towards 'A'. This approach is particularly useful when the processing of an element depends on the elements that come after it.
Precomputation
A powerful approach, especially for problems involving summation or multiplication of subarrays. This method involves computing some information in advance (before the main part of the algorithm) and storing it for quick access. This precomputed information is often in the form of prefix sums, suffix sums, or similar constructs. Let's break down this concept:
Key Concepts:
Prefix Sum/Product: This involves creating an array where each element at index
irepresents the sum (or product) of all elements from the start of the array up to indexi. This allows for quick calculation of the sum of any subarray.Suffix Sum/Product: Similar to the prefix sum, but each element at index
irepresents the sum (or product) of all elements from indexito the end of the array.
Example : Given the original array: [3, 1, 4, 1, 5, 9, 2], the correct Prefix Sum array should be calculated as follows:
Original Array:
[3, 1, 4, 1, 5, 9, 2]Prefix Sum Array:
Element 0:
3(just the first element)Element 1:
3 + 1 = 4Element 2:
3 + 1 + 4 = 8Element 3:
3 + 1 + 4 + 1 = 9Element 4:
3 + 1 + 4 + 1 + 5 = 14Element 5:
3 + 1 + 4 + 1 + 5 + 9 = 23Element 6:
3 + 1 + 4 + 1 + 5 + 9 + 2 = 25
So, the Prefix Sum array is: [3, 4, 8, 9, 14, 23, 25]
Now, if you want to find the sum of elements from index 2 to 5 in the original array, you can subtract the prefix sum at index 1 from the prefix sum
at index 5: 23 - 4 = 19.
Hashing: Sometimes, especially with more complex operations or conditions, a hash table (or dictionary) is used to store precomputed values for quick lookup.
Hashing, particularly using a hash table or dictionary, is a technique where you store data in a way that enables very fast retrieval. In the context of array processing, hashing is often used to precompute and store values for quick lookup later.
Example Problem:
Suppose you have an array, and you want to find out if there are any duplicate elements in it.
Traditional Approach:
You might iterate over the array and, for each element, check the rest of the array for duplicates. This approach can be inefficient, especially for large arrays, as it has a time complexity of O(n²).
Using Hashing:
Instead, you can use a hash table (or a dictionary in some languages) to solve this problem more efficiently.
Steps Using Hashing:
1. **Create an Empty Hash Table**: This will store elements of the array as keys.
2. **Iterate Over the Array**: For each element:
- Check if the element is already in the hash table.
- If it is, you've found a duplicate.
- If it's not, add the element to the hash table.
3. **Complete the Iteration**: If you finish iterating without finding duplicates, there are no duplicates in the array.
function hasDuplicate(arr) {
const hashTable = {};
for (let i = 0; i < arr.length; i++) {
if (hashTable[arr[i]]) {
return true; // Duplicate found
}
hashTable[arr[i]] = true; // Store the element in the hash table
}
return false; // No duplicates found
}
// Example usage
const array = [1, 2, 3, 4, 5, 1];
console.log(hasDuplicate(array)); // Output: true, because '1' is a duplicate
```
Explanation:
- We use a JavaScript object `hashTable` as our hash table.
- As we iterate over the array, we check if each element is already a key in `hashTable`.
- If an element is found in `hashTable`, it means we've seen this element before, and thus it's a duplicate.
- If it's not found, we add it to `hashTable`.
- This approach has a time complexity of O(n), which is more efficient than the traditional approach.
Hashing is a powerful technique for problems where you need to efficiently check for the presence of items, count items, or find duplicates. By using a hash table, you can reduce the time complexity of these operations, making your algorithms faster and more efficient.
Index as a hash key
The concept of using an array index as a hash key for in-place modifications is a clever technique often used in algorithmic problems, especially when you're required to solve a problem with constant space complexity (O(1) space).
Example:
The First Missing Positive problem is an algorithm problem that requires finding the smallest positive integer that is not present in a given unsorted array of integers. The goal is to find the missing positive integer with the least value in the array in O(n) time complexity and O(1) space complexity.
For example, if your array is [3, 4, -1, 1], the smallest positive number not in the array is 2.
Concept
Array as a Hash Table: You use the indices of the array as if they were keys in a hash table.
In-Place Modification: Instead of using extra space, you modify the original array to record information.
Example Scenario
Problem: Find the first missing positive number in an array.
Given: An array of integers, where the values range from 1 to N (N is the length of the array).
Simplified Example
Array:
[3, 4, -1, 1]Process:
Value 3: Negate value at index 2 (
arr[2]becomes negative).Value 4: Ignore as it's outside the range 1 to N.
Value -1: Ignore as it's negative.
Value 1: Negate value at index 0 (
arr[0]becomes negative).
Result: The array becomes
[-3, 4, -1, -1].First Missing Positive: The first index with a positive value is 1 (second element), so the first missing positive number is 2.Caveats
Caveats
Destructive: This method modifies the original array, which might not be acceptable in all cases.
Essential questions
Resources:
https://www.coursera.org/learn/data-structures/lecture/OsBSF/arrays
https://dev.to/liaowow/understanding-the-sliding-window-technique-in-algorithms-206o
In the second blog post we will discuss techniques about how to think in each of the Essential questions, stay tuned …