Intro.
Time Complexity:
To determine the time complexity of different algorithms, we use Big O notation, which provides an upper bound on the growth rate of the algorithm as the input size increases. The notation is denoted can be imagined like: O(f(n)), where "f(n)" represents the function that describes the upper bound on the algorithm's time complexity.
O(1) - Constant Time Complexity: The algorithm's execution time remains constant regardless of the input size.
O(n) - Linear Time Complexity: The algorithm's execution time grows linearly with the input size.
O(n^2)- Quadratic Time Complexity: The algorithm's execution time grows quadratically with the input size.O(log n),it means that the execution time of the algorithm grows logarithmically with the input size (n). In other words, as the input size increases, the execution time increases at a slower rate compared to linear growth (O(n)) or quadratic growth (O(n^2)).5. O(2^n) - Exponential Time Complexity: The algorithm's execution time grows exponentially with the input size. Very inefficient for large inputs:
Each function call branches into two recursive calls.
Hence the tree would look like the one below for 'n' equals 5.
Full Article resource : Full Article
Explore time complexity analysis with different data structures :
QUEUE:
Remember : In a linked list implementation of a queue, the dequeue operation typically happens at the head of the list. The reason for this is that in a queue, elements are removed in the order in which they were added, which is known as the "first-in-first-out" (FIFO)

10 as the first element in the list. The head pointer points to the first node in the list.To dequeue an element from the list, we need to remove the first node (10) and update the head pointer to point to the second node (20).
After the dequeue operation, the linked list would look like this:

10) has been removed, and the head pointer now points to the second node (20).Time required to dequeue an element is constant and does not depend on the size of the queue.
This is because removing an element from the head of a linked list simply involves updating the head pointer to point to the next node in the list and freeing the memory allocated for the removed node. These operations can be performed in constant time, regardless of the size of the list.
Linked list :
if the case is : insertion
We have to traverse from the head of the list until you reach the desired node. This traversal takes linear time and has a time complexity of O(n).
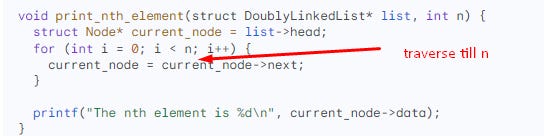
function first gets the head of the list and then traverses the list until it reaches the nth element. Once it reaches the nth element, it prints the data of the node. Explore time complexity analysis with Functions:
1- Example 1:
The time complexity of setting the value of the nth element in a linked list is O(1). This is because we already have a pointer to the node to set the value of, so we can simply update the value of the node in O(1) time.
Example 2:
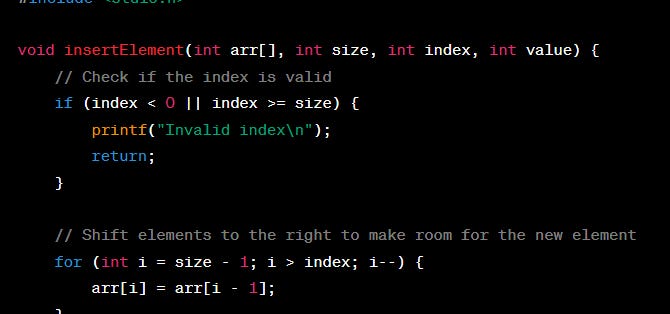
algorithm must iterate through the array, starting from the element after the one that is being shifted, and copying each element one position to the right. The operation of shifting elements inside the array takes constant time for each element that needs to be moved, regardless of the size of the array. So, the loop's time complexity is proportional to the number of elements shifted.
Therefore, the time complexity of inserting an element into an unsorted array at a specific index is O(N), where N is the number of elements currently in the array. It's important to note that this time complexity remains the same regardless of the position where you insert the element (beginning, middle, or end) since the shifting operation covers the same number of elements in any case.
Remove node: Traverse till previous node to update its pointer to point to node next to node removed.
Hash Tables:
Best case: The element being inserted has a unique hash value, and the hash table is not full. In this case, the insertion operation takes a constant amount of time, O(1).
Worst case: The element being inserted has a hash value that collides with the hash value of another element in the hash table, and the hash table is full. In this case, the insertion operation takes linear time, O(n).
See Part 1:













awesome thought process on the white board
Amazing blog, thanks a lot, it help a lot <3
nuuX