Strings- Concept And Techniques
A comprehensive guide on various strings operations and techniques used in algorithm design, particularly for solving problems efficiently - KMP - Rabin-Karp
Intro
What is a String?
Imagine a string as a necklace of letters, like `"Hello World"`. Each letter is a bead on this necklace.
Immutability: Can't Change a Bead
- **Explanation**: In many languages, you can't change a bead (character) in a necklace (string). If you want a different bead, you make a new necklace.
- **Example**: Changing `"cat"` to `"bat"` means creating a new string `"bat"`, not just swapping 'c' for 'b'.
Character Encoding: The Bead Shapes
- **Explanation**: Each bead (character) has a unique shape (encoding like ASCII or Unicode). Some shapes are simple (1 byte), others complex (multiple bytes).
- **Example**: ASCII uses simple shapes (like 'A', 'B', 'C'), Unicode includes complex shapes (like emojis 😊).
Common Operations: Necklace Tricks
- **Concatenation**: Joining two necklaces into one, like `"Hello " + "World"` becomes `"Hello World"`.
- **Substring**: Taking a part of the necklace, `"Hello".substring(0, 2)` gives `"He"`.
- **Searching**: Finding a bead, `"Hello".indexOf('e')` tells you 'e' is the second bead.
String Length: Counting Beads
- **Explanation**: Just count the beads (characters) in the necklace (string).
- **Example**: The length of `"Hello"` is 5.
Traversal and Access: Walking Along the Necklace
- **Traversal**: Looking at each bead one by one.
- **Access**: Picking a specific bead, like the 3rd bead in `"Hello"` is `'l'`.
Comparison: Matching Necklaces
- **Explanation**: Check if two necklaces are the same by comparing each bead.
- **Example**: `"Hello"` and `"hello"` are different (case-sensitive).
Substring and Pattern Matching: Finding Patterns in Necklaces
- **Brute-force**: Check every possible combination.
- **KMP Algorithm**: A smarter way to skip some checks.
Mutability Workarounds: Making a Changeable Necklace
- **Explanation**: Use a special box (like StringBuilder in Java) to assemble a necklace you can change.
- **Example**: Adding 's' to `"String"` to make `"Strings"`.
Space Complexity: The Box Size
- **Explanation**: Every new necklace needs space. Be mindful of how many necklaces you make!
Language-Specific Features: Special Necklace Tools
- **Python Slicing**: Cutting parts of the necklace easily like `"Hello"[1:4]` gives `"ell"`.
- **JavaScript Template Literals**: Combining necklaces with variables easily.
Regular Expressions: The Necklace Pattern Guide
- **Explanation**: A set of rules to describe patterns in necklaces.
- **Example**: Finding phone numbers in a text.
Edge Cases: Special Necklaces
- **Empty String**: A necklace with no beads.
- **Single Character**: A necklace with one bead.
- **Special Characters**: Necklaces with beads like spaces or punctuation.
Rabin-Karp Algorithm: Rolling Hash Magic
The Rabin-Karp Algorithm is a string-searching algorithm that uses hashing to find any one of a set of pattern strings in a text. It's particularly effective in situations where the same text is searched for multiple patterns simultaneously.
“The basic idea of the Rabin-Karp algorithm is to use a hash function to compute a fingerprint for each substring of the text. The fingerprint for a substring is a unique number that represents the substring. The algorithm then compares the fingerprints of the substrings of the text to the fingerprints of the patterns. If the fingerprints of a substring and a pattern match, the algorithm reports that the pattern has been found in the text.”
Here's a breakdown of how it works, tailored to your background in software engineering:
Concept
1. **Hash Function**: Rabin-Karp uses a hash function to convert each substring of the text and the pattern into a numerical value. The idea is that it's faster to compare integers than strings.
2. **Rolling Hash**: The algorithm uses a rolling hash technique to efficiently compute the hash value of the next substring from the current substring's hash value.
Process
1. **Initial Hashing**:
- Compute the hash value of the pattern.
- Compute the hash value of the first substring of the text (the substring's length is equal to the pattern's length).
2. **Sliding the Window**:
- Slide the window one character at a time over the text.
- For each new window, update the hash value (using the rolling hash technique).
- Compare the hash value of the current substring with the hash value of the pattern.
3. **Hash Match**:
- When a match is found (hash values are equal), compare the actual substring and the pattern to verify the match (to handle hash collisions).
4. **Continue Until End**:
- Continue this process until the end of the text.
Advantages
- **Efficient for Multiple Pattern Search**: Particularly efficient when the same text is searched for different patterns.
- **Time Complexity**: Best and average case time complexity is
O(n+m)where n is the length of the text and m is the length of the pattern.
Disadvantages
- **Hash Collisions**: Different strings can have the same hash value. When a hash match occurs, the algorithm must check for actual equality.
- **Worst-Case Time Complexity**: In the worst case (many collisions), the time complexity can degrade to
O(nm).
Implementation
In C or Python, the implementation involves creating a function for the rolling hash and then iterating over the text to compare hash values. Python's dynamic typing and high-level functions can make the implementation more straightforward, while in C, you'd manage more details like character-to-integer conversion and modulo arithmetic for the hash function.
Use Cases
- **Plagiarism Detection**: Commonly used in detecting plagiarism where multiple patterns (documents) are searched in large texts.
- **String Matching in DNA Sequences**: Used in bioinformatics for searching specific sequences in DNA.
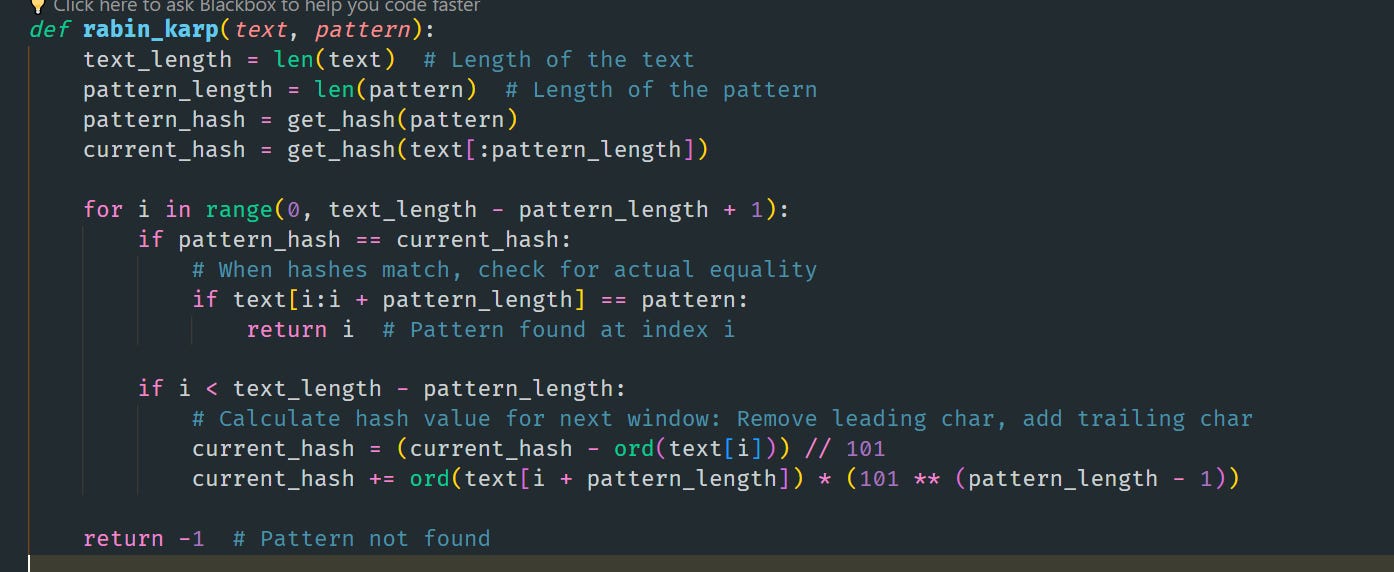
"ABCCDEFGH" and the pattern "CDE". The length of the text is 9, and the length of the pattern is 3. When i is 6 ("FGH"), 6 < 9 - 3 is True, so we can update the hash for the next window.When i is 7 ("GH" and part of the text is outside the window), 7 < 9 - 3 is False, so we should not attempt to update the hash as there's no sufficient substring left.Note:
The ord() function in Python is a built-in function that returns an integer representing the Unicode code point of the given Unicode character. This function is commonly used to convert a character into its corresponding ASCII (or Unicode) numerical value.
Hash Function:
The `get_hash` function is a crucial part of the Rabin-Karp algorithm, as it computes the hash value of a given string. Here's a breakdown of its implementation:
```python
def get_hash(s, prime=101):
h = 0
for i in range(len(s)):
h = (h * 256 + ord(s[i])) % prime
return h
```
In this `get_hash` function:
- `prime` is a prime number used as the modulus to ensure the hash value stays within a reasonable range and to reduce the likelihood of hash collisions.
- `256` is used as the base for the hash calculation, which corresponds to the number of characters in the extended ASCII table. This choice is arbitrary and could be any number, but using 256 allows for a good distribution of hash values for strings.
- `ord(s[i])` converts the character `s[i]` to its ASCII integer value.
- The hash `h` is calculated using a rolling method, where it's continuously multiplied by the base (256) and then added to the ASCII value of the current character, ensuring that each character in the string affects the final hash value.
- The `% prime` operation is applied at each step to keep the hash value within a fixed range and to avoid integer overflow.
The rolling hash is computed in such a way that it can be easily updated when we move to the next window in the text, which is an essential part of the Rabin-Karp algorithm's efficiency. The `get_hash` function encapsulates this logic for initializing the hash values of the pattern and the first window of the text.
KMP Algorithm
The Knuth-Morris-Pratt (KMP) algorithm is a string searching (or pattern matching) algorithm that improves the efficiency of searching for a pattern in a text by avoiding unnecessary comparisons. This is achieved through the use of a precomputed "failure function" or "prefix table."
First thing to understand:
Phase 1 : LPS Array:
The LPS array is used to skip comparisons while matching a pattern in a string. When a mismatch occurs after some matches, we know that characters of the pattern before the mismatched character will not match. The LPS array helps to find the next position in the pattern to start the comparison, skipping unnecessary comparisons.
Example:
Let's consider the pattern "AAACAAAA".
For the substring
"A", there is no proper prefix which is also a suffix. So,lps[0] = 0.For
"AA", the longest proper prefix which is also a suffix is"A". So,lps[1] = 1.For
"AAA", it's"AA". So,lps[2] = 2.For
"AAAC", there is no such proper prefix. So,lps[3] = 0.For
"AAACA", the longest proper prefix which is also a suffix is"A". So,lps[4] = 1.For
"AAACAA", it's"AA". So,lps[5] = 2.For
"AAACAAA", it's"AAA". So,lps[6] = 3.Finally, for
"AAACAAAA", it's"AAAA". So,lps[7] = 4.
So, the LPS array for "AAACAAAA" is [0, 1, 2, 0, 1, 2, 3, 4].
Phase 2 : Searching Phase:
Pattern Matching:
The pattern is aligned with the beginning of the text.
Characters are matched from left to right.
When a mismatch occurs, the lps table is used to find the next position in the pattern that should be compared to the current character in the text. This step is crucial as it prevents unnecessary comparisons.
This process is repeated until either the pattern is found in the text or the text is completely searched.
Example
Let's say we have a text T = "ABABDABACDABABCABAB" and we want to search for a pattern P = "ABABCABAB" using the KMP algorithm.
LPS Array: Phase:
Construct lps table for pattern
P = "ABABCABAB".The lps array would be
[0, 0, 1, 2, 0, 1, 2, 3, 4].
Searching Phase:
Start comparing pattern
Pwith textTfrom the left.When the first mismatch is encountered, use the lps table to shift the pattern.
For example, if a mismatch occurs at position 7 in
P, instead of moving the pattern one position to the right, we can skip to position 3 (as per the lps table).
This method of skipping comparisons greatly improves the efficiency of the search, especially when the pattern has repeated sub-patterns. The KMP algorithm runs in O(n) time complexity, where n is the length of the text, which is a significant improvement over the naïve search algorithm.
Resources:


