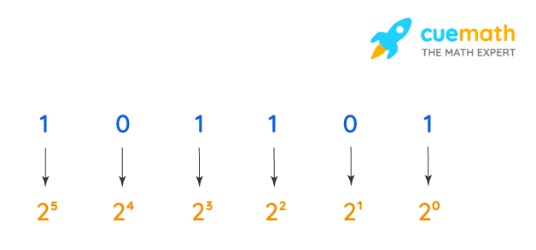
What is Binary?
Binary is a way of representing numbers using only two digits: 0 and 1. It's different from the decimal system that we use daily, which has ten digits (0 to 9).
In computing, binary is used because computers operate with two states: on and off. These states can be easily represented as 1 (on) and 0 (off).
Counting in Binary:
In decimal, you count from 0 to 9, and then go to 10. In binary, you only have 0 and 1. When you run out of digits, you add another column to the left. So you count like this: 0, 1, and then you add a column for 2 (which is 10 in binary), then 11 (3 in decimal), 100 (4 in decimal), and so on.
Let's convert the decimal number 174 to binary:
Converting Binary to Decimal:
Bits and Bytes:
A bit is the smallest unit of data in binary, which can be either a 0 or a 1.
A byte is made up of 8 bits. Bytes are the basic building blocks of data storage and processing in computers.
Binary Addition
Shifting:
Imagine people standing in a line where each person represents a digit in a binary number. A shift to the left means everyone takes a step to their left, and a new person (a zero) joins at the right end of the line. A shift to the right means everyone takes a step to the right, and the person at the far left leaves the line. Each step represents a multiplication or division by two, depending on the direction of the shift.
Shifting in binary numbers is similar to shifting positions in a line of people or moving decimal places in numbers.
Analogy: Imagine people standing in a line where each person represents a digit in a binary number. A shift to the left means everyone takes a step to their left, and a new person (a zero) joins at the right end of the line. A shift to the right means everyone takes a step to the right, and the person at the far left leaves the line. Each step represents a multiplication or division by two, depending on the direction of the shift.
Binary Shifting Examples:
1.Left Shift (<<): A left shift in binary is like moving all the digits in a number one position to the left and filling the new rightmost position with a 0.
In terms of value, each left shift doubles the number (multiplies it by 2).
For example, take the binary number 101 (which is 5 in decimal):
When we shift 101 to the left by one position, we get 1010. We've effectively multiplied the original number by 2.
Right Shift (>>): A right shift is the opposite, where we move all digits in a number one position to the right and drop the rightmost digit.
In terms of value, each right shift halves the number (divides it by 2, discarding any remainder).
For instance, let's shift the binary number 1010 (which is 10 in decimal) to the right:
Significant Note: There are two types of right shifts in computing:
Logical right shift: Fills the leftmost position with 0, regardless of the number's sign.
Arithmetic right shift: Fills the leftmost position with the sign bit (0 for positive, 1 for negative numbers) to preserve the sign of the number.
Masks
In computing, masks are used to manage and manipulate specific bits within a binary number. A mask is a binary number that is combined with another binary number using a bitwise operation such as AND, OR, XOR, or NOT.
The purpose of using a mask is to isolate, set, clear, or toggle individual bits or groups of bits in a binary number.
Here's an explanation of each type of bitwise operation used with masks:
1. **AND Masking:**
Used to clear bits (set them to 0).
- The mask has bits set to 1 for every bit that should remain unchanged, and bits set to 0 for every bit that should be cleared.
- Example: Clearing the last 3 bits of `11111111` with an AND mask `11111000` results in `11111000`.
2. **OR Masking:**
Used to set bits (turn them to 1).
- The mask has bits set to 1 for every bit that should be set, and bits set to 0 for every bit that should remain unchanged.
- Example: Setting the last 3 bits of `11111000` with an OR mask `00000111` results in `11111111`.
3. **XOR Masking:**
Used to toggle bits (flip them from 0 to 1 or 1 to 0).
- The mask has bits set to 1 for every bit that should be toggled, and bits set to 0 for every bit that should remain unchanged.
- Example: Toggling the last 3 bits of `11111000` with an XOR mask `00000111` results in `11111111`.
4. NOT Masking:
Used to invert all bits (turning all 0s to 1s and all 1s to 0s).
- It is a unary operation, which means it only requires one operand, the number itself.
- Example: Inverting `11110000` with a NOT operation results in `00001111`.
Masks are especially useful in embedded systems, graphics, cryptography, and anywhere binary data needs to be manipulated at the bit level. By using masks, a programmer can easily manipulate bits for controlling hardware, setting configurations, or optimizing the performance of algorithms that operate at the bit level.
Thanks to
for the following brief :AND: 1 only if both bits are 1
OR: 1 if any of the two bits is 1
XOR: 1 if the two bits are different
NOT: inverts all bits
Use bitwise operations to calculate the sum.
It calculates the sum of the numbers without taking into account the carry, then calculates the carry using bitwise AND and shift left operator, and finally adds the sum and carry together.
whileloop, which will continue to iterate as long asbis not equal to 0.Inside the loop, the sum of
aandbis calculated without the carry. This is done using the XOR bitwise operation (a ^ b). The XOR operation effectively adds the bits where there's a difference (i.e., where one bit is 1 and the other is 0).Then, it calculates the carry that would result from adding
aandb. This is done using the AND bitwise operation (a & b) and then left-shifting the result by one (<< 1). The carry is the result of bits that are both 1 in the same position inaandb, as adding 1 and 1 in binary would result in a carry.The sum without the carry (from step 3) is assigned to
a.The carry (from step 4) is assigned to
b.The loop continues, now adding the new
a(previous sum without carry) and newb(carry from the previous addition). This is because the carry may produce a new carry when added to the sum.