Algorithmic Techniques For Arrays

How to think - learn techniques - Arrays

Dec 15, 2023

How to think ?

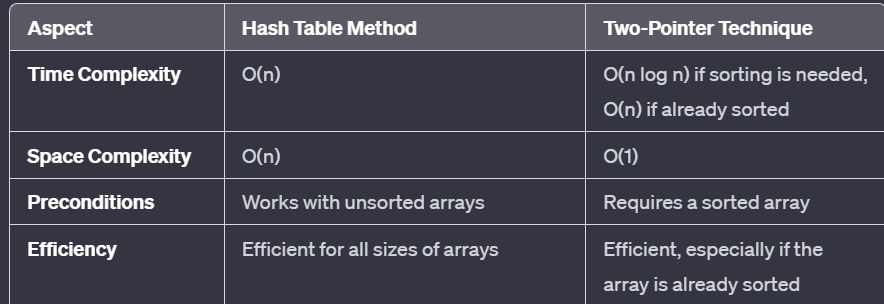
Sorted or not sorted ?

If the array is already sorted, the Two-Pointer Technique is an excellent choice for the Two Sum problem. If the array is not sorted, the Hash Table Method is generally the better choice for the Two Sum problem. This method offers a good balance between time efficiency and simplicity.

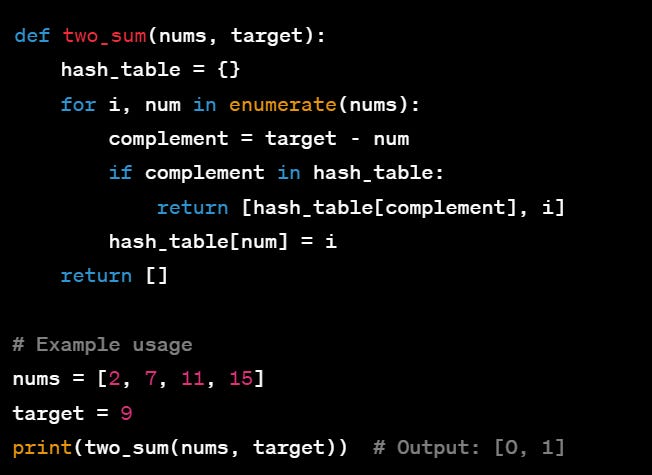
Let's go through a numerical example to illustrate how the hash table evolves as we solve the Two Sum problem using the Hash Table Method.

Problem Setup

- **Array (`nums`):** `[2, 7, 11, 15]`
- **Target (`target`):** `9`
Goal : Find indices of two numbers in `nums` such that they add up to `target`.

Process and Hash Table Evolution

1. **Initialize an empty hash table.** - Hash Table: `{}`

2. **Iterate through the array.**

- **First Element:** `2`

- Complement = `9 - 2 = 7`

- Complement `7` is not in the hash table.

- Add `2` to the hash table with its index: `{2: 0}`

- **Second Element:** `7`

- Complement = `9 - 7 = 2`

- Complement `2` is in the hash table.

- Pair found: `2` (index 0) and `7` (index 1).

Result

- **Indices:** `[0, 1]` (indices of `2` and `7` in the array)

- **Explanation:** `nums[0] + nums[1] = 2 + 7 = 9`, which is the target.

Python Code Snippet

Time Complexity: O(n), where n is the number of elements in the array. Each element is processed exactly once.—— Space Complexity: O(n), for the hash table. In the worst case, it stores n key-value pairs (if no pair is found).

In this example, the hash table helps us quickly check whether the complement of each number (needed to reach the target) has already been seen in the array. Once we find such a complement, we immediately have our solution.

See Code in Js

2- Best Time to Buy and Sell Stock

The best technique to solve this problem, often referred to as the "Best Time to Buy and Sell Stock" problem, is to use a single-pass approach that keeps track of the minimum price seen so far and the maximum profit that can be achieved.

This method is efficient and straightforward, with a time complexity of O(n), where n is the number of days (or the length of the `prices` array).

Approach

1. **Initialize Two Variables:**

- `min_price`: Set it to an initially high value (e.g., `float('inf')` in Python).

- `max_profit`: Set it to 0.

2. **Iterate Through the Array:**

- For each price `p` in `prices`:

- Update `min_price` if `p` is less than the current `min_price`.

- Calculate the profit if you were to sell the stock on this day (`p - min_price`).

- Update `max_profit` if this profit is greater than the current `max_profit`.

3. **Return `max_profit`:**

- After iterating through the array, `max_profit` will contain the maximum profit achievable.

Python Implementation

Example : prices = [7, 1, 5, 3, 6, 4]

let's walk through the code with a numerical example to illustrate how the iterations work. Consider the following array of stock prices:

prices = [7, 1, 5, 3, 6, 4]

The goal is to find the maximum profit from buying and selling the stock on different days.

Iterations Explained with the Example

Initialize Variables:
- min_price = float('inf') (A very large number)
- max_profit = 0
First Iteration (price = 7):
- min_price = min(inf, 7) = 7
- profit = 7 - 7 = 0
- max_profit = max(0, 0) = 0
Second Iteration (price = 1):
- min_price = min(7, 1) = 1
- profit = 1 - 1 = 0
- max_profit = max(0, 0) = 0

And so on….Final Result => After iterating through all the prices, the max_profit is 5, which is the maximum profit achievable from this transaction.

- **Single Pass:** The array is traversed only once, making the algorithm efficient.

Complexity

- **Time Complexity:** O(n), as we go through the array once.
- **Space Complexity:** O(1), as only two variables (`min_price` and `max_profit`) are used, regardless of the input size.

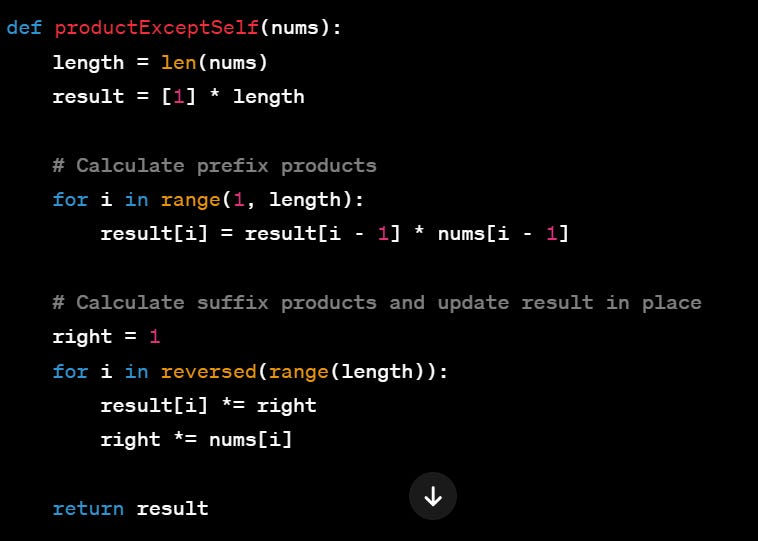
3- Product of Array Except Self:

Both the prefix (left-to-right) and suffix (right-to-left) approaches have the same time complexity, which is O(n), where n is the number of elements in the array. Since the time complexity is the same for both methods, the choice between them often comes down to implementation preference or specific problem constraints.

Example Iteration for Suffix Products

Initial State:
- nums = [4, 5, 1, 3]
- result = [1, 4, 20, 20] (after calculating prefix products)
- right = 1
Iteration for i = 3:
- result[3] is 20. Multiply it by right (1): result[3] = 20 * 1 = 20.
- Update right: right = 1 * nums[3] = 1 * 3 = 3.
Iteration for i = 2:
- result[2] is 20. Multiply it by right (3): result[2] = 20 * 3 = 60.
- Update right: right = 3 * nums[2] = 3 * 1 = 3.
Iteration for i = 1:
- result[1] is 4. Multiply it by right (3): result[1] = 4 * 3 = 12.
- Update right: right = 3 * nums[1] = 3 * 5 = 15.
Iteration for i = 0:
- result[0] is 1. Multiply it by right (15): result[0] = 1 * 15 = 15.

Final Result

result = [15, 12, 60, 20]

Explanation

In each iteration, right represents the product of all elements to the right of the current index i.
By multiplying result[i] with right, we effectively get the product of all elements in the array except nums[i].
This method ensures that each element in the result array is the product of all other elements in nums, excluding itself.

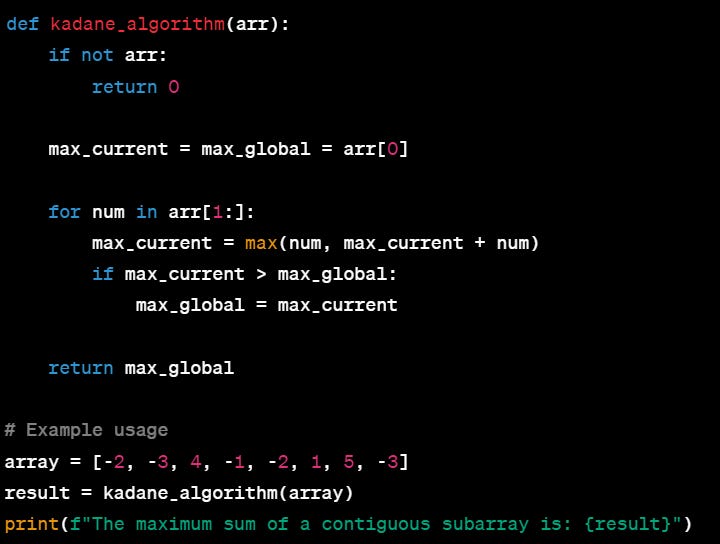
4- Maximum Sub Array : Kadane's Algorithm

Kadane's Algorithm is a dynamic programming approach used to find the maximum sum contiguous subarray within a one-dimensional array of numbers. This algorithm is particularly well-suited for problems where you need to find a contiguous subarray (sequence of elements) with the largest sum in a given array, and it's a common question in FAANG (Facebook, Amazon, Apple, Netflix, Google) interviews.

Time Complexity:

O(n), where n is the number of elements in the array. This is because the algorithm only needs to traverse the array once.

Space Complexity:

O(1), as it only requires a few variables to store the current sum, maximum sum, and sometimes the start and end indices of the maximum subarray.

Basic Concept:

Objective: Find the maximum sum of a contiguous subarray in an array of integers.
Key Insight: The maximum sum at any position is either the current element itself or the sum of the current element and the maximum sum up to the previous position.

Example:

Let's go through a numerical example to illustrate how Kadane's Algorithm works. Consider the following array:

Array: [-2, -3, 4, -1, -2, 1, 5, -3]

We'll apply Kadane's Algorithm to find the maximum sum contiguous subarray:

Initialize Variables:
- max_current = max_global = -2 (first element of the array)
Iterate Through the Array:
- Element -3: max_current becomes max(-3, -2 - 3) = -3, max_global remains -2
- Element 4: max_current becomes max(4, -3 + 4) = 4, max_global is updated to 4
- Element -1: max_current becomes max(-1, 4 - 1) = 3, max_global remains 4
- Element -2: max_current becomes max(-2, 3 - 2) = 1, max_global remains 4
- Element 1: max_current becomes max(1, 1 + 1) = 2, max_global remains 4
- Element 5: max_current becomes max(5, 2 + 5) = 7, max_global is updated to 7
- Element -3: max_current becomes max(-3, 7 - 3) = 4, max_global remains 7
Result:
- The max_global value after completing the iteration is 7.

Thus, the maximum sum of a contiguous subarray in this array is 7. The subarray contributing to this sum is [4, -1, -2, 1, 5].

Kadane's Algorithm efficiently finds this maximum sum by dynamically updating the max_current and max_global values while traversing the array only once. This example demonstrates its effectiveness, even with arrays containing both positive and negative numbers.

During each iteration, it updates max_current to be the maximum of the current element and the sum of max_current and the current element.
If max_current is greater than max_global, it updates max_global.